MADE: Benchmark Environments for Closed-Loop Materials Discovery

Existing benchmarks for computational materials discovery primarily evaluate static predictive tasks or isolated computational sub-tasks. While valuable, these evaluations neglect the inherently iterative and adaptive nature of scientific discovery. We introduce MAterials Discovery Environments (MADE), a novel framework for benchmarking end-to-end autonomous materials discovery pipelines. MADE simulates closed-loop discovery campaigns in which an agent or algorithm proposes, evaluates, and refines candidate materials under a constrained oracle budget, capturing the sequential and resource-limited nature of real discovery workflows. We formalize discovery as a search for thermodynamically stable compounds relative to a given convex hull, and evaluate efficacy and efficiency via comparison to baseline algorithms. The framework is flexible; users can compose discovery agents from interchangeable components such as generative models, filters, and planners, enabling the study of arbitrary workflows ranging from fixed pipelines to fully agentic systems with tool use and adaptive decision making. We demonstrate this by conducting systematic experiments across a family of systems, enabling ablation of components in discovery pipelines, and comparison of how methods scale with system complexity.

DeePM: Regime-Robust Deep Learning for Systematic Macro Portfolio Management

We propose DeePM (Deep Portfolio Manager), a structured deep-learning macro portfolio manager trained end-to-end to maximize a robust, risk-adjusted utility. DeePM addresses three fundamental challenges in financial learning: (1) it resolves the asynchronous "ragged filtration" problem via a Directed Delay (Causal Sieve) mechanism that prioritizes causal impulse-response learning over information freshness; (2) it combats low signal-to-noise ratios via a Macroeconomic Graph Prior, regularizing cross-asset dependence according to economic first principles; and (3) it optimizes a distributionally robust objective where a smooth worst-window penalty serves as a differentiable proxy for Entropic Value-at-Risk (EVaR) - a window-robust utility encouraging strong performance in the most adverse historical subperiods. In large-scale backtests from 2010-2025 on 50 diversified futures with highly realistic transaction costs, DeePM attains net risk-adjusted returns that are roughly twice those of classical trend-following strategies and passive benchmarks, solely using daily closing prices. Furthermore, DeePM improves upon the state-of-the-art Momentum Transformer architecture by roughly fifty percent. The model demonstrates structural resilience across the 2010s "CTA (Commodity Trading Advisor) Winter" and the post-2020 volatility regime shift, maintaining consistent performance through the pandemic, inflation shocks, and the subsequent higher-for-longer environment. Ablation studies confirm that strictly lagged cross-sectional attention, graph prior, principled treatment of transaction costs, and robust minimax optimization are the primary drivers of this generalization capability.

Training Instabilities Induce Flatness Bias in Gradient Descent

Classical analyses of gradient descent (GD) define a stability threshold based on the largest eigenvalue of the loss Hessian, often termed sharpness. When the learning rate lies below this threshold, training is stable and the loss decreases monotonically. Yet, modern deep networks often achieve their best performance beyond this regime. We demonstrate that such instabilities induce an implicit bias in GD, driving parameters toward flatter regions of the loss landscape and thereby improving generalization. The key mechanism is the Rotational Polarity of Eigenvectors (RPE), a geometric phenomenon in which the leading eigenvectors of the Hessian rotate during training instabilities. These rotations, which increase with learning rates, promote exploration and provably lead to flatter minima. This theoretical framework extends to stochastic GD, where instability-driven flattening persists and its empirical effects outweigh minibatch noise. Finally, we show that restoring instabilities in Adam further improves generalization. Together, these results establish and understand the constructive role of training instabilities in deep learning.

Can Stability be Detrimental? Better Generalization through Gradient Descent Instabilities

Traditional analyses of gradient descent optimization show that, when the largest eigenvalue of the loss Hessian - often referred to as the sharpness - is below a critical learning-rate threshold, then training is 'stable' and training loss decreases monotonically. Recent studies, however, have suggested that the majority of modern deep neural networks achieve good performance despite operating outside this stable regime. In this work, we demonstrate that such instabilities, induced by large learning rates, move model parameters toward flatter regions of the loss landscape. Our crucial insight lies in noting that, during these instabilities, the orientation of the Hessian eigenvectors rotate. This, we conjecture, allows the model to explore regions of the loss landscape that display more desirable geometrical properties for generalization, such as flatness. These rotations are a consequence of network depth, and we prove that for any network with depth > 1, unstable growth in parameters cause rotations in the principal components of the Hessian, which promote exploration of the parameter space away from unstable directions. Our empirical studies reveal an implicit regularization effect in gradient descent with large learning rates operating beyond the stability threshold. We find these lead to excellent generalization performance on modern benchmark datasets.

Few-Shot Learning Patterns in Financial Time-Series for Trend-Following Strategies

Forecasting models for systematic trading strategies do not adapt quickly when financial market conditions change, as was seen in the advent of the COVID-19 pandemic in 2020, when market conditions changed dramatically causing many forecasting models to take loss-making positions. To deal with such situations, we propose a novel time-series trend-following forecaster that is able to quickly adapt to new market conditions, referred to as regimes. We leverage recent developments from the deep learning community and use few-shot learning. We propose the Cross Attentive Time-Series Trend Network - X-Trend - which takes positions attending over a context set of financial time-series regimes. X-Trend transfers trends from similar patterns in the context set to make predictions and take positions for a new distinct target regime. X-Trend is able to quickly adapt to new financial regimes with a Sharpe ratio increase of 18.9% over a neural forecaster and 10-fold over a conventional Time-series Momentum strategy during the turbulent market period from 2018 to 2023. Our strategy recovers twice as quickly from the COVID-19 drawdown compared to the neural-forecaster. X-Trend can also take zero-shot positions on novel unseen financial assets obtaining a 5-fold Sharpe ratio increase versus a neural time-series trend forecaster over the same period. X-Trend both forecasts next-day prices and outputs a trading signal. Furthermore, the cross-attention mechanism allows us to interpret the relationship between forecasts and patterns in the context set.

SANE: The phases of gradient descent through Sharpness Adjusted Number of Effective parameters

Modern neural networks are undeniably successful. Numerous studies have investigated how the curvature of loss landscapes can affect the quality of solutions. In this work we consider the Hessian matrix during network training. We reiterate the connection between the number of "well-determined" or "effective" parameters and the generalisation performance of neural nets, and we demonstrate its use as a tool for model comparison. By considering the local curvature, we propose Sharpness Adjusted Number of Effective parameters (SANE), a measure of effective dimensionality for the quality of solutions. We show that SANE is robust to large learning rates, which represent learning regimes that are attractive but (in)famously unstable. We provide evidence and characterise the Hessian shifts across "loss basins" at large learning rates. Finally, extending our analysis to deeper neural networks, we provide an approximation to the full-network Hessian, exploiting the natural ordering of neural weights, and use this approximation to provide extensive empirical evidence for our claims.

On Sequential Bayesian Inference for Continual Learning

Sequential Bayesian inference can be used for continual learning to prevent catastrophic forgetting of past tasks and provide an informative prior when learning new tasks. We revisit sequential Bayesian inference and test whether having access to the true posterior is guaranteed to prevent catastrophic forgetting in Bayesian neural networks. To do this we perform sequential Bayesian inference using Hamiltonian Monte Carlo. We propagate the posterior as a prior for new tasks by fitting a density estimator on Hamiltonian Monte Carlo samples. We find that this approach fails to prevent catastrophic forgetting demonstrating the difficulty in performing sequential Bayesian inference in neural networks. From there we study simple analytical examples of sequential Bayesian inference and CL and highlight the issue of model misspecification which can lead to sub-optimal continual learning performance despite exact inference. Furthermore, we discuss how task data imbalances can cause forgetting. From these limitations, we argue that we need probabilistic models of the continual learning generative process rather than relying on sequential Bayesian inference over Bayesian neural network weights. In this vein, we also propose a simple baseline called Prototypical Bayesian Continual Learning, which is competitive with state-of-the-art Bayesian continual learning methods on class incremental continual learning vision benchmarks.

Statistical Design and Analysis for Robust Machine Learning: A Case Study from COVID-19

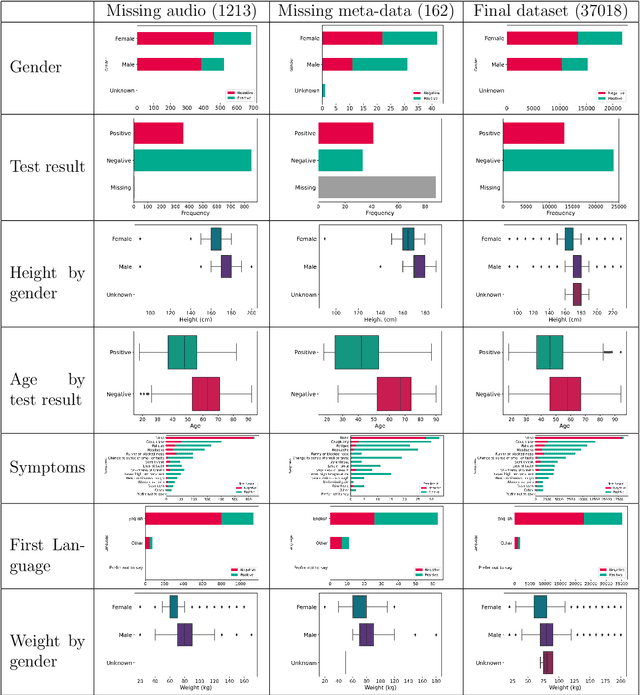
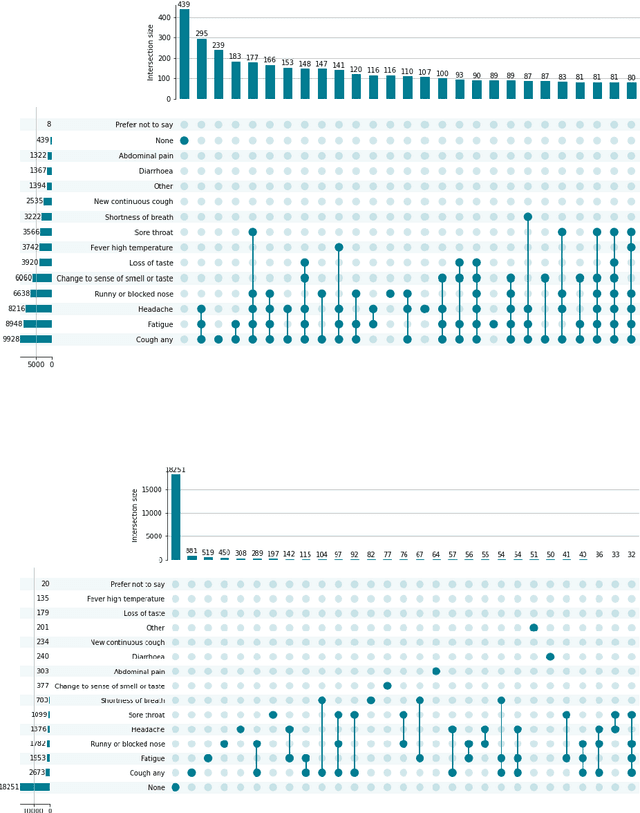
Since early in the coronavirus disease 2019 (COVID-19) pandemic, there has been interest in using artificial intelligence methods to predict COVID-19 infection status based on vocal audio signals, for example cough recordings. However, existing studies have limitations in terms of data collection and of the assessment of the performances of the proposed predictive models. This paper rigorously assesses state-of-the-art machine learning techniques used to predict COVID-19 infection status based on vocal audio signals, using a dataset collected by the UK Health Security Agency. This dataset includes acoustic recordings and extensive study participant meta-data. We provide guidelines on testing the performance of methods to classify COVID-19 infection status based on acoustic features and we discuss how these can be extended more generally to the development and assessment of predictive methods based on public health datasets.

The Surprising Effectiveness of Latent World Models for Continual Reinforcement Learning

We study the use of model-based reinforcement learning methods, in particular, world models for continual reinforcement learning. In continual reinforcement learning, an agent is required to solve one task and then another sequentially while retaining performance and preventing forgetting on past tasks. World models offer a task-agnostic solution: they do not require knowledge of task changes. World models are a straight-forward baseline for continual reinforcement learning for three main reasons. Firstly, forgetting in the world model is prevented by persisting existing experience replay buffers across tasks, experience from previous tasks is replayed for learning the world model. Secondly, they are sample efficient. Thirdly and finally, they offer a task-agnostic exploration strategy through the uncertainty in the trajectories generated by the world model. We show that world models are a simple and effective continual reinforcement learning baseline. We study their effectiveness on Minigrid and Minihack continual reinforcement learning benchmarks and show that it outperforms state of the art task-agnostic continual reinforcement learning methods.

Learning General World Models in a Handful of Reward-Free Deployments

Building generally capable agents is a grand challenge for deep reinforcement learning (RL). To approach this challenge practically, we outline two key desiderata: 1) to facilitate generalization, exploration should be task agnostic; 2) to facilitate scalability, exploration policies should collect large quantities of data without costly centralized retraining. Combining these two properties, we introduce the reward-free deployment efficiency setting, a new paradigm for RL research. We then present CASCADE, a novel approach for self-supervised exploration in this new setting. CASCADE seeks to learn a world model by collecting data with a population of agents, using an information theoretic objective inspired by Bayesian Active Learning. CASCADE achieves this by specifically maximizing the diversity of trajectories sampled by the population through a novel cascading objective. We provide theoretical intuition for CASCADE which we show in a tabular setting improves upon na\"ive approaches that do not account for population diversity. We then demonstrate that CASCADE collects diverse task-agnostic datasets and learns agents that generalize zero-shot to novel, unseen downstream tasks on Atari, MiniGrid, Crafter and the DM Control Suite. Code and videos are available at https://ycxuyingchen.github.io/cascade/